I have dealt with hand inspection over the past five years and I quickly learned how to check precision bores using three pin gauges. With extreme care, this method can save from having a custom gauge for every one-off bore that the engineers specify and allow for accurate measurement of small bores (less than 2 inches). The Machinists Handbook has a general formula that gives a simple way to find a set of three pins to use, however, it usually only gets you close, which is what a pair of calipers does. In a nut shell, I made my own Pin Gauge Finder program that will find the best set of three pin gauges in seconds for a desired bore size. You can find the program I made at the link below. Sorry for it being hosted on Source Forge, please be careful where you click.
https://sourceforge.net/projects/pin-gauge-finder/
Notes for the Pin Gauge user:
- Pin gages are almost always 60 HRC (hardened steel) and have sharp edges. They can easily scratch softer materials as you slide them in a bore. Depending on the purpose of the bore, you may not want to use the three-pin method.
- No pin gauge is exactly a given diameter, they each have an individual tolerance. Conveniently, working through the math, the outer Soddy circle diameter tolerance ends up being only 2 times the pin tolerance.
If you are interested in more information, please continue reading.
Background History
The history goes back to ancient Greece in the second century BC, with the Apollonus circle problem. René Descartes first gave a solution in the 1600’s via a quadratic equation. Frederick Soddy rediscovered the solution in the 1930’s and published it in the form of a poem, The Kiss Precise, which described the solution to the special case of three circles all touching each other. The solution can be expressed neatly in terms of the curvature of the circles, k, which is the inverse of the radius:
![]()
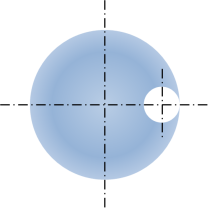
There are two possible solutions, the inner and outer Soddy circles, where the outer Soddy circle is essentially a bore. Rearranging the solution and replacing the curvatures with pin diameters [Dp1, Dp2, Dp3] gives the solution for the outer Soddy circle of diameter Dia. Dia will be a negative number as the three pins are internal to it.
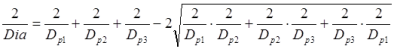
Before I go much further in how to solve this equation, we need to look at how many possible combinations there are for a given pin gauge set. This can be done by using the combination formula.
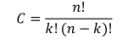
Where n is the number of pins available and k is the size of the group, in our case, 3 pins. Looking at a typical high quality pin gauge set where the maximum diameter pin is 25 mm, minimum diameter pin is 5 mm, and step size between pins is 0.01 mm, then there are 1,333,333,000 unique pin combinations. This is quite a large number for a standard computer to process, so further refinement needs to be done.
One can take the following steps to reduce the possible combinations to search:
- Set Dp1 > Dp2 > Dp3
- This ensures that only unique solutions (all 1.3 billion of them) are searched
- Solve Descartes theorem for Pin 3 (Dp3)
- Focus on the square root
- Dia is a given, so for any value of Dp1, one can find the maximum Dp2 value that keeps the term under the square root positive.
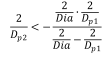
- Since Dp2 > Dp3, the minimum value of Dp2 is found by solving the Descartes theorem with Dp3 = Dp2.
- Focus on the pin range.
- This is somewhat obvious. Don’t calculate if any pin falls outside the available pin range.
With this approach, for a given Dia, one can cycle through a small range of Dp2 pins for each Dp1 pin, and then only two or three Dp3 pins for each Dp2 pin. Overall, for the given pin range mentioned above, this brought the maximum number of iterations performed to 249,705; a much more reasonable number that can be performed in mere seconds.
The Beauty of it All
As I was optimizing the program, I noticed that the solutions tended to fall on a 3-dimensional surface. I plotted the solutions as a point cloud, with each axis representing a pin and each point colored based on its error. For a given diameter, the surface would intuitively move from one bounded corner to the other as shown below.
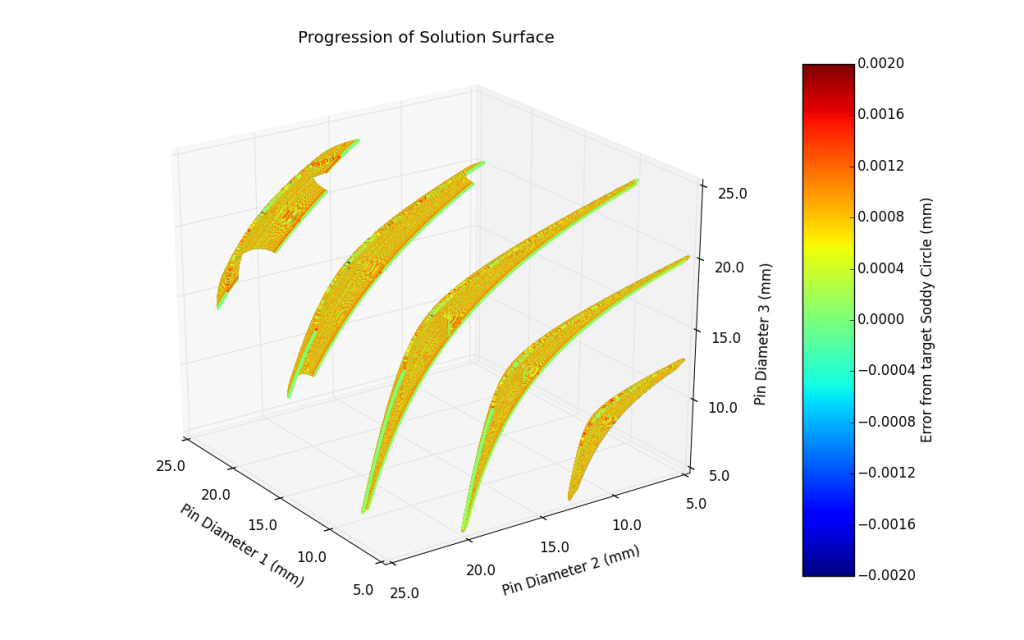
Rotating the view to look normal to the surfaces, fascinating patterns are created.
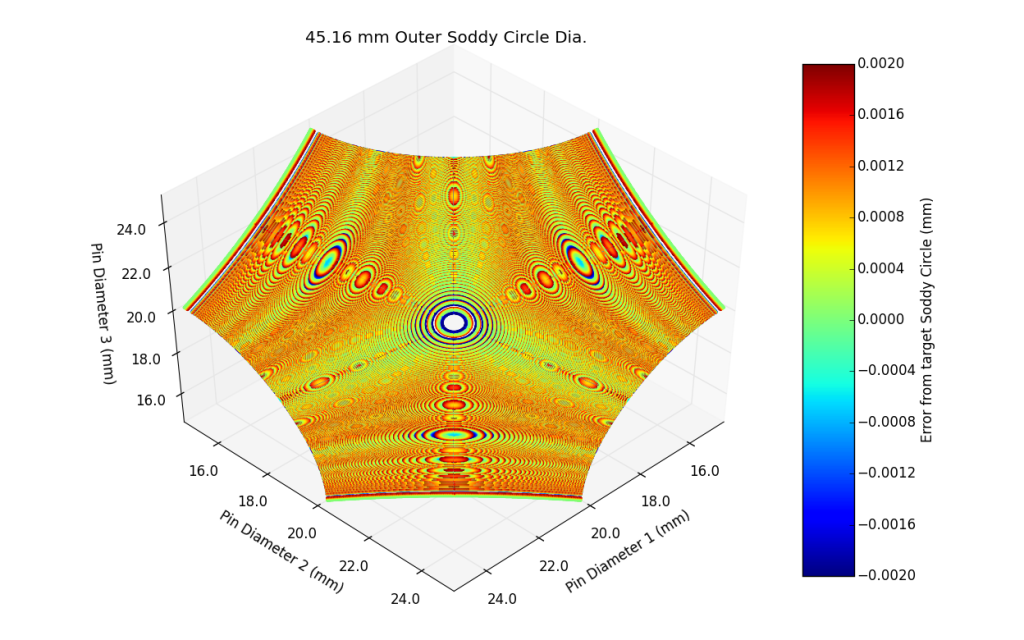
While I initially thought that the solutions fell on a sphere, it turns out they fall on some sort of 3-Dimensional 3-cusped hypocycloid. To illustrate this further, below is a video of the pin gauge set mentioned above, and the surfaces created from the range of outer Soddy Circles.
This just shows how unexpected things can come out of mundane efforts.
Fitting Points to a Sphere
I think it’s worthy to mention that while researching efficient ways to fit the solutions to a sphere, I stumbled on the below matrix technique[1] that works if you have a minimum of n=9 points:
![]()
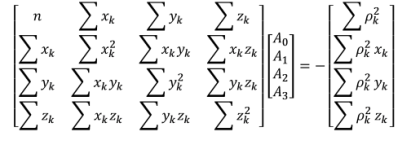
where the coordinates of the sphere center [a,b,c] and sphere radius, R, are given by:
![]()
This is an easy algorithm to program for large data sets and worked great as I was playing with large data sets (~30,000 points).
More information and useful links can be found here:
[1] Régressions coniques, quadriques, circulaire, sphérique. QUADRATURE. No. 65, July 2007. pg 4-5.
Descartes Circle Theorem on Mathworld
Marv Klotz’s Utilities – lots of useful DOS programs, including a brute force Plug.zip program that does the same thing but much slowly
Permutation Formula on MathWords
Combination Formula on MathWords
And bonus reading (and maybe a future post) on Triangle centers:
Soddy Centers on Mathworld
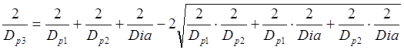
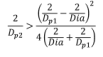
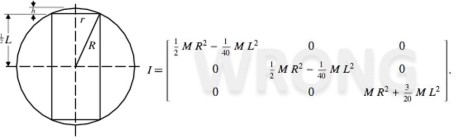
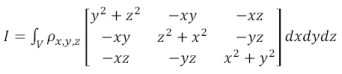 (1)
(1)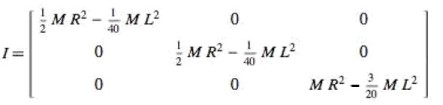

 Many brush-on paints exists to cover galvanized steel, but spray paints appear to be non-existent. After much research, I finally found the solution. Acryllic latex will adhere to galvanized steel with minimal surface preparation. Therefore, the solution is
Many brush-on paints exists to cover galvanized steel, but spray paints appear to be non-existent. After much research, I finally found the solution. Acryllic latex will adhere to galvanized steel with minimal surface preparation. Therefore, the solution is